Variational perturbation theory

In mathematics, variational perturbation theory (VPT) is a mathematical method to convert divergent power series in a small expansion parameter, say

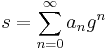$s=\sum_{n=0}^\infty a_n g^n$ ,

into a convergent series in powers

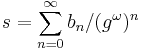$s=\sum_{n=0}^\infty b_n /(g^\omega)^n$ ,

where $\omega$ is a critical exponent (the so-called index of "approach to scaling" introduced by Franz Wegner). This is possible with the help of variational parameters, which are determined by optimization order by order in $g$ . The partial sums are converted to convergent partial sums by a method developed in 1992^[1].

Most perturbation expansions in quantum mechanics are divergent for any small coupling strength $g$. They can be made convergent by VPT (for details see the first textbook cited below). The convergence is exponentially fast^[2] ^[3].

After its success in quantum mechanics, VPT has been developed further to become an important mathematical tool in quantum field theory with its anomalous dimensions^[4]. Applications focus on the theory of critical phenomena. It has led to the most accurate predictions of critical exponents. More details can be read here.

References

^ Kleinert, H. (1995). "Systematic Corrections to Variational Calculation of Effective Classical Potential". Phys. Lett. A 173: 332. http://users.physik.fu-berlin.de/~kleinert/213/213.pdf.
^ Kleinert H. and Janke W. (1993). "Convergence Behavior of Variatioal Perturbation Expansion - A Method for Locating Bender-Wu Singularities". Phys. Lett. A 206: 283. http://users.physik.fu-berlin.de/~kleinert/235/235.pdf.
^ Guida R., Konishi K., and Suzuki H. (1996). "Systematic Corrections to Variational Calculation of Effective Classical Potential". Ann. Phys. (N.Y.) 249: 109. http://www.sciencedirect.com/science?_ob=MImg&_imagekey=B6WB1-45V7F53-22-1&_cdi=6697&_user=1676895&_pii=S0003491696900664&_origin=search&_coverDate=07%2F10%2F1996&_sk=997509998&view=c&wchp=dGLbVtz-zSkzk&md5=161cd093bb98727f8731cd5c96190848&ie=/sdarticle.pdf.
^ Kleinert H. (1998). "Strong-coupling behavior of φ^4 theories and critical exponents". Phys. Rev. D 57: 2264. Bibcode 1998PhRvD..57.2264K. doi:10.1103/PhysRevD.57.2264. http://users.physik.fu-berlin.de/~kleinert/257/257.pdf.

References

Kleinert H., Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 3. Auflage, World Scientific (Singapore, 2004) (readable online here) (see Chapter 15)
Kleinert H. and Verena Schulte-Frohlinde, Critical Properties of φ⁴-Theories, World Scientific (Singapur, 2001); Paperback ISBN 981-02-4658-7 (readable online here) (see Chapter 19)
Feynman, Richard P.; Kleinert, Hagen (1986), "Effective classical partition functions", Phys. Rev., A 34 (6): 5080–5084, December 1986, Bibcode 1986PhRvA..34.5080F, doi:10.1103/PhysRevA.34.5080, PMID 9897894